Business Finance Homework Help

I have to respond to the discussion as well as 2 students

This Unit’s Discussion Topics

Choose one of the following to respond to:

1. Discuss the measures of risk. What are they? What are the advantages/disadvantages of them?
2. Discuss the risk and return trade-off. What type of relationship do they have? When is risk a good thing vs. a bad thing?
3. What is risk? What does it mean to be risk averse? Why do companies have different levels of risk aversion?
4. Discuss decision trees including their key components, how they are used and the benefits companies get from them.

Student 1

Good Morning Class,

Discuss decision trees including their key components, how they are used and the benefits companies get from them.

A decision tree is a support tool that models probable outcomes and highlights differences between specific choices. Once the outcomes are laid out, they can be made and presented similar to a tree-like structure. Decision trees highlight a decision-making steps that can lead to a favorable result. Decision trees typically have 3 main components; the root (decision node), the branch (chance nodes), and the leaf (end node). The root node, is the starting question, expressed as the starting point of the tree. Chance nodes represent probability or uncertainty. Thus the leaf or end node, represent the outcome. The three nodes outline the flow from question to answer. There can be multiple internal nodes, which represent the chance nodes. An example of a decision tree utilized in everyday life is below.

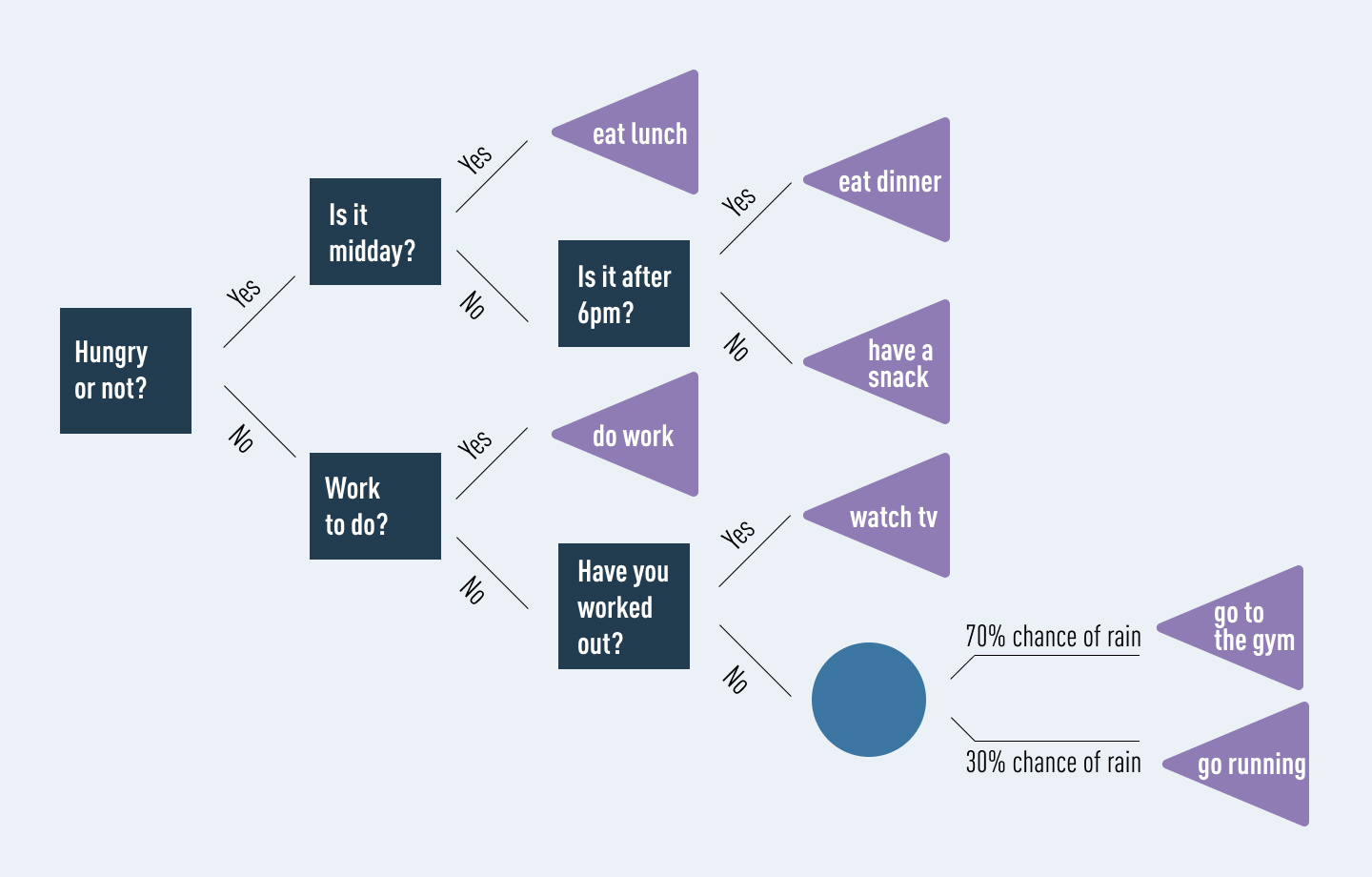
Decision trees can also be similarly utilized to highlight key determinants within investment or capital project decisions. Within a business, the same flow and outline is used to determine the expected outcomes of undertaking (or not undertaking) particular courses of action. Once the probabilities of successes and failures are determined, decision trees can help clarify the expected value of capital budgeting decisions. Decision trees in financial analysis are a net present value calculation that incorporates different future scenarios based on how likely they are to occur. The cash flows for a given decision are the sum of cash flows for all alternative options, weighted based on their probability. “Companies often accept what initially seems like negatives NPV projects, but once the real option value is considered, the NPV actually becomes positive (Pinkasovitch 2021).” Decision trees will not provide a full proof answer or course of action. Instead, they outline a direction that management can take that will give the maximum return, based on all of the available information at that time.

undefined

References:

Block, S., Hirt, G., & Danielsen, B. (2017). Foundations of Financial Management. (16th ed.). McGraw Hill.

Pinkasovitch, A. (2021 Jan. 14). Using Decision Trees in Finance. Article posted to investopedia.com. Retrieved on 2021 May 4 from https://www.investopedia.com/articles/financial-theory/11/decisions-trees-finance.asp

Student 2

Discuss the measures of risk. What are they? What are the advantages/disadvantages of them?

Risk is the probability of loss and is often measured in terms of losses and uncertainty. To quantitatively measure risk, an analyst can use the coefficient of variation or the beta. Alternatively, an analyst may want to evaluate risk using qualitative measures using risk classes.

To find the coefficient of variation, the expected value and standard deviation must first be computed. The expected value of an investment can be determined by weighing the average of outcomes with their probability of occurring. The formula is D bar (expected value) = ∑DP, where D is the outcome possibilities and P is the probability that the outcome will occur. After determining the expected value, an analyst can determine the standard deviation, or the amount of variation around the expected value. This can be found using the equation σ (standard deviation) = SqRt[∑(D – Dbar)2P], where D is the outcome possibilities, Dbar is the expected value, and P is the probability that the outcome will occur. The standard deviation allows an analyst to understand how spread out the outcomes may be in comparison to the expected value. This measure can be useful in determining investment volatility. A higher standard deviation will indicate greater risk associated with that investment. In other words, it tells investors how uncertain it is that the expected value of the investment will be attained. However, this measure is only useful if the expected values of investments being compared are the same. In order to compare investments with different expected values with the standard deviation measure, the coefficient of variation must be used. The formula for this coefficient is V (coefficient of variation) = σ / Dbar, where σ is the standard deviation and Dbar is the expected value of the investment. Using the resulting measures, investments can be compared in terms of risk. This method of evaluating risk can be useful because of the consistency that it provides. Unfortunately, this method also become less reliable the further out one tries to forecast. This is due to the increased uncertainty related to the passage of time (Block, 2016). The standard deviation and coefficient of variation also assumes a normal distribution (i.e., bell curve), which is not always the case. For example, hedge fund investments are often skewed in one direction, making the measure less applicable (Deviation Risk Measure, n.d.).

The beta measure is often used to determine the volatility of individual stock returns when compared to the overall market. For instance, the S&P 500 Index has a beta of 1.0. When an individual stock fluctuates more than the market, its beta is greater than 1, and when it fluctuates less than the market, its beta is less than one. Therefore, if a stock’s beta is 0.30, an investor can make the assumption that the stock is a fairly stable and low-risk investment. Because of it’s simple, easy-to-understand, and quantifiable nature, the beta measure is a very popular measure of risk. One of the biggest drawbacks of using beta to determine risk is that it does not provide a clear picture of the business, as it is too simplified. Critics argue that the measure is best used for short-term, rather than long-term, investments (McClure, 2020).

Risk classes are a way of qualitatively measuring risk by adjusting the discount rate with the perceived level of risk for the activity. For example, a low to no risk investment class, such as repairing old equipment, would have a lower adjusted discount rate than a high risk investment class, such as investing in a new market. This type of risk measurement is useful because it takes into consideration factors that may not be quantifiable. Unfortunately, it is also based on perception, so it may be harder to ascertain the reliability of the measures (Block, 2016).

References

Block, S. (2016). Foundations of Financial Management. [MBS Direct]. Retrieved from

https://mbsdirect.vitalsource.com/#/books/9781259357534/ (Links to an external site.)

Deviation Risk Measure. (n.d.). Corporate Finance Institute. Retrieved from https://corporatefinanceinstitute.com/resources/knowledge/trading-investing/deviation-risk-measure/ (Links to an external site.)

McClure, B. (2020, February 18). What Beta Means When Considering a Stock’s Risk. Investopedia. Retrieved from https://www.investopedia.com/investing/beta-know-risk/